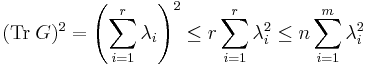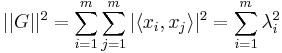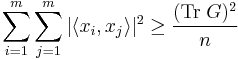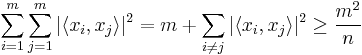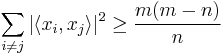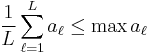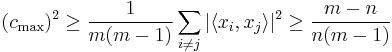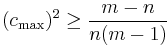Welch bounds
In mathematics, Welch bounds are a family of inequalities pertinent to the problem of evenly spreading a set of unit vectors in a vector space. The bounds are important tools in the design and analysis of certain methods in telecommunication engineering, particularly in coding theory. The bounds were originally published in a 1974 paper by L. R. Welch.
Contents |
Mathematical statement
If 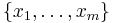 are unit vectors in
are unit vectors in 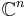 , define
, define 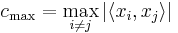 , where
, where 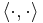 is the usual inner product on
is the usual inner product on 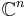 . Then the following inequalities hold for
. Then the following inequalities hold for 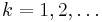 :
:
Applicability
If 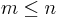 , then the vectors
, then the vectors 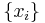 can form an orthonormal set in
can form an orthonormal set in 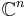 . In this case,
. In this case, 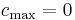 and the bounds are vacuous. Consequently, interpretation of the bounds is only meaningful if
and the bounds are vacuous. Consequently, interpretation of the bounds is only meaningful if 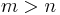 . This will be assumed throughout the remainder of this article.
. This will be assumed throughout the remainder of this article.
Proof for k = 1
The "first Welch bound," corresponding to 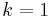 , is by far the most commonly used in applications. Its proof proceeds in two steps, each of which depends on a more basic mathematical inequality. The first step invokes the Cauchy-Schwarz inequality and begins by considering the
, is by far the most commonly used in applications. Its proof proceeds in two steps, each of which depends on a more basic mathematical inequality. The first step invokes the Cauchy-Schwarz inequality and begins by considering the 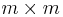 Gram matrix
Gram matrix  of the vectors
of the vectors 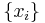 ; i.e.,
; i.e.,
The trace of  is equal to the sum of its eigenvalues. Because the rank of
is equal to the sum of its eigenvalues. Because the rank of  is at most
is at most  , and it is a positive semidefinite matrix,
, and it is a positive semidefinite matrix,  has at most
has at most  positive eigenvalues with its remaining eigenvalues all equal to zero. Writing the non-zero eigenvalues of
positive eigenvalues with its remaining eigenvalues all equal to zero. Writing the non-zero eigenvalues of  as
as  with
with 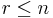 and applying the Cauchy-Schwarz inequality to the inner product of an
and applying the Cauchy-Schwarz inequality to the inner product of an  -vector of ones with a vector whose components are these eigenvalues yields
-vector of ones with a vector whose components are these eigenvalues yields
The square of the Frobenius norm (Hilbert–Schmidt norm) of  satisfies
satisfies
Taking this together with the preceding inequality gives
Because each  has unit length, the elements on the main diagonal of
has unit length, the elements on the main diagonal of  are ones, and hence its trace is
are ones, and hence its trace is 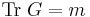 . So,
. So,
or
The second part of the proof uses an inequality encompassing the simple observation that the average of a set of non-negative numbers can be no greater than the largest number in the set. In mathematical notation, if 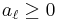 for
for 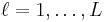 , then
, then
The previous expression has 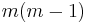 non-negative terms in the sum,the largest of which is
non-negative terms in the sum,the largest of which is 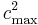 . So,
. So,
or
which is precisely the inequality given by Welch in the case that 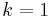
Achieving Welch bound equality
In certain telecommunications applications, it is desirable to construct sets of vectors that meet the Welch bounds with equality. Several techniques have been introduced to obtain so-called Welch Bound Equality (WBE) sets of vectors for the k = 1 bound.
The proof given above shows that two separate mathematical inequalities are incorporated into the Welch bound when 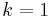 . The Cauchy–Schwarz inequality is met with equality when the two vectors involved are collinear. In the way it is used in the above proof, this occurs when all the non-zero eigenvalues of the Gram matrix
. The Cauchy–Schwarz inequality is met with equality when the two vectors involved are collinear. In the way it is used in the above proof, this occurs when all the non-zero eigenvalues of the Gram matrix  are equal, which happens precisely when the vectors
are equal, which happens precisely when the vectors 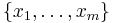 constitute a tight frame for
constitute a tight frame for 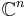 .
.
The other inequality in the proof is satisfied with equality if and only if 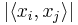 is the same for every choice of
is the same for every choice of 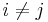 . In this case, the vectors are equiangular. So this Welch bound is met with equality if and only if the set of vectors
. In this case, the vectors are equiangular. So this Welch bound is met with equality if and only if the set of vectors 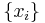 is an equiangular tight frame in
is an equiangular tight frame in 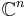 .
.
References
- S. Datta, S. D. Howard, and D. Cochran, “Geometry of the Welch Bounds,” http://arxiv.org/abs/0909.0206v1
- L. R. Welch, “Lower Bounds on the Maximum Cross Correlation of Signals,” IEEE Trans. on Info. Theory, vol. 20, no. 3, pp. 397–399, May 1974.
![(c_\max)^{2k} \geq \frac{1}{m-1} \left[ \frac{m}{\binom{n%2Bk-1}{k}}-1 \right]](/2012-wikipedia_en_all_nopic_01_2012/I/a6a2e8ffc75e064b8bba76abc324e9a9.png)
![G=\left[ \begin{array}{ccc} \langle x_1, x_1 \rangle & \cdots & \langle x_1, x_m \rangle \\ \vdots & \ddots & \vdots \\ \langle x_m, x_1 \rangle & \cdots & \langle x_m, x_m \rangle \end{array}\right]](/2012-wikipedia_en_all_nopic_01_2012/I/b03d03b1051f91b4b665931ea9cd1f4c.png)